GAMES101 作业8 质点弹簧系统 踩坑指南

Posted on |

依赖库安装

使用以下命令安装

1
sudo apt install libglu1-mesa-dev freeglut3-dev mesa-common-dev xorg-dev

不要直接从pdf上复制命令，pdf上的横线符号是错误的，会导致 unable to locate

段错误

来自在 Win10 下配置 GAMES101 开发环境（WSL2） - 知乎 (zhihu.com)
1.执行

1
export LIBGL_ALWAYS_INDIRECT=0

2.下载MobaXterm，作为终端启动ropesim

但是，我的MobaXterm中只有一个WSL，上文提到图形界面显示失败的问题并未解决。

下面是通过StackOverflow等摸索而来：

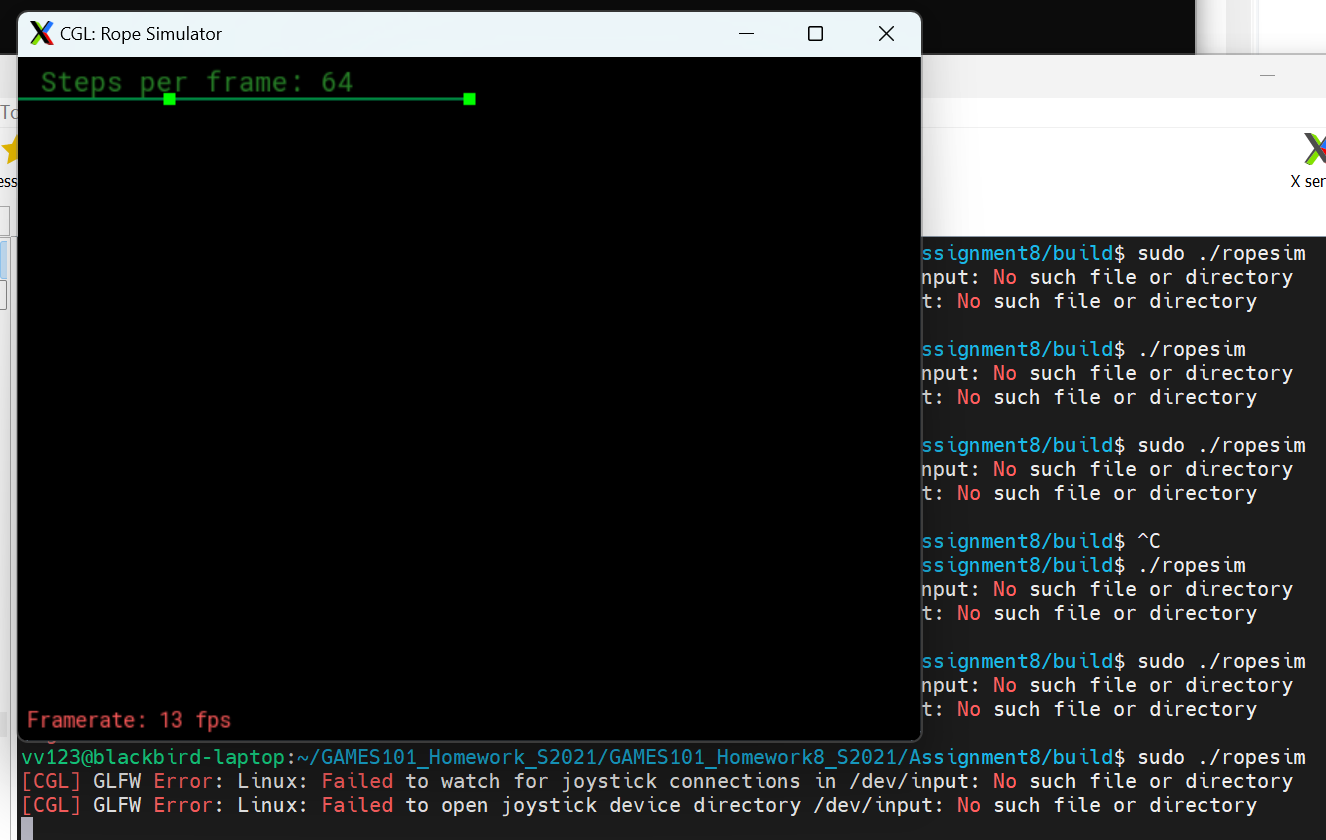
GLFW Error: Linux: Failed to watch for joystick…

执行

1
touch ~/.Xauthority

然后重启MobaXterm，

然后执行

1
sudo cp ~/.Xauthority  /root/

然后使用sudo打开ropesim

1
sudo ./ropesim

虽然仍会显示GLFW Error,但能够成功显示窗口。

image-20240528170135716

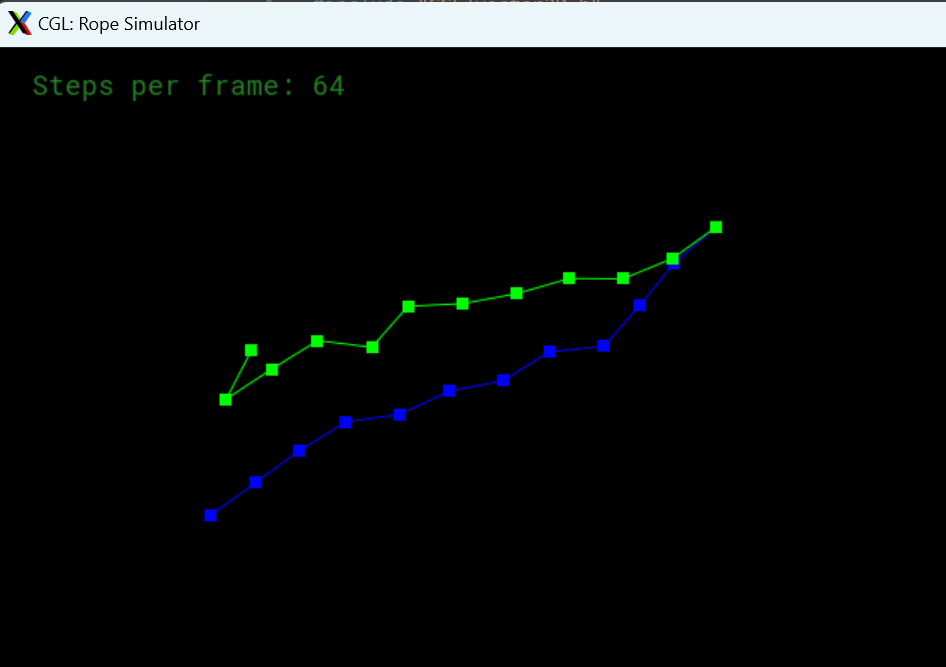
弹簧乱飞

参考：

关于作业8的一些问题解答 – 计算机图形学与混合现实在线平台 (games-cn.org)

对于显示欧拉法，是正常的，减小步长（如 sudo ./ropesim -s 1024 ）可以减缓发散的时间（但还是会发散）

对于Verlet方法，要在计算每个质点后把 m->forces清零，上面simulateEuler函数中已经给出，此处需要自己加上。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <iostream>
#include <vector>

#include "CGL/vector2D.h"

#include "mass.h"
#include "rope.h"
#include "spring.h"

namespace CGL {

    Rope::Rope(Vector2D start, Vector2D end, int num_nodes, float node_mass, float k, vector<int> pinned_nodes)
    {
        // TODO (Part 1): Create a rope starting at `start`, ending at `end`, and containing `num_nodes` nodes.


        // Def of rope:
        // vector<Mass *> masses;
        // vector<Spring *> springs;

        /*
          Mass(Vector2D position, float mass, bool pinned)
      : start_position(position), position(position), last_position(position),
        mass(mass), pinned(pinned) {}
        Spring(Mass *a, Mass *b, float k)
      : m1(a), m2(b), k(k), rest_length((a->position - b->position).norm()) {}
        */
        for (int i = 0; i < num_nodes; i++) {
            Vector2D pos = start + (end - start) * (1.0 * i / (num_nodes - 1));
            masses.emplace_back(new Mass(pos, node_mass, false));
        }

        for (int i = 0; i < num_nodes - 1; i++) {
            springs.emplace_back(new Spring(masses[i], masses[i + 1], k));
        } 

        // Comment-in this part when you implement the constructor
        for (auto &i : pinned_nodes) {
            masses[i]->pinned = true;
        }
    }

    void Rope::simulateEuler(float delta_t, Vector2D gravity)
    {
        for (auto &s : springs)
        {
            // TODO (Part 2): Use Hooke's law to calculate the force on a node
            auto len = (s->m1->position - s->m2->position).norm();
            s->m1->forces += - s->k * (s->m1->position - s->m2->position) / len * (len - s->rest_length);
            s->m2->forces += - s->k * (s->m2->position - s->m1->position) / len * (len - s->rest_length);
        }

        for (auto &m : masses)
        {
            if (!m->pinned)
            {
                // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position
                auto a = m->forces / m->mass + gravity;
                float kd = 0.005; a += - kd * m->velocity / m->mass;  // TODO (Part 2): Add global damping
                auto v_t = m->velocity;
                m->velocity += a * delta_t;
                //m->position += v_t * delta_t;  //Explicit Method 不收敛
                m->position += m->velocity * delta_t; // Semi-implicit method
            }

            // Reset all forces on each mass
            m->forces = Vector2D(0, 0);
        }
    }

    void Rope::simulateVerlet(float delta_t, Vector2D gravity)
    {
        for (auto &s : springs)
        {
            // TODO (Part 3): Simulate one timestep of the rope using explicit Verlet （solving constraints)
            auto len = (s->m1->position - s->m2->position).norm();
            s->m1->forces += -s->k * (s->m1->position - s->m2->position) / len * (len - s->rest_length);
            s->m2->forces += -s->k * (s->m2->position - s->m1->position) / len * (len - s->rest_length);
        }

        for (auto &m : masses)
        {
            if (!m->pinned)
            {
                Vector2D temp_position = m->position;
                // TODO (Part 3.1): Set the new position of the rope mass
                // TODO (Part 4): Add global Verlet damping
                auto a = m->forces / m->mass + gravity;
                float damping_factor = 0.00000000005;
                m->position = temp_position + (1 - damping_factor) * (temp_position - m->last_position) + a * delta_t * delta_t; 
                m->last_position = temp_position;
            }
            m->forces = Vector2D(0, 0);
        }
    }
}

image-20240528180227291